How to put boundaries on infinity?
Compactification
Let’s first imagine an infinite grid of space and time.
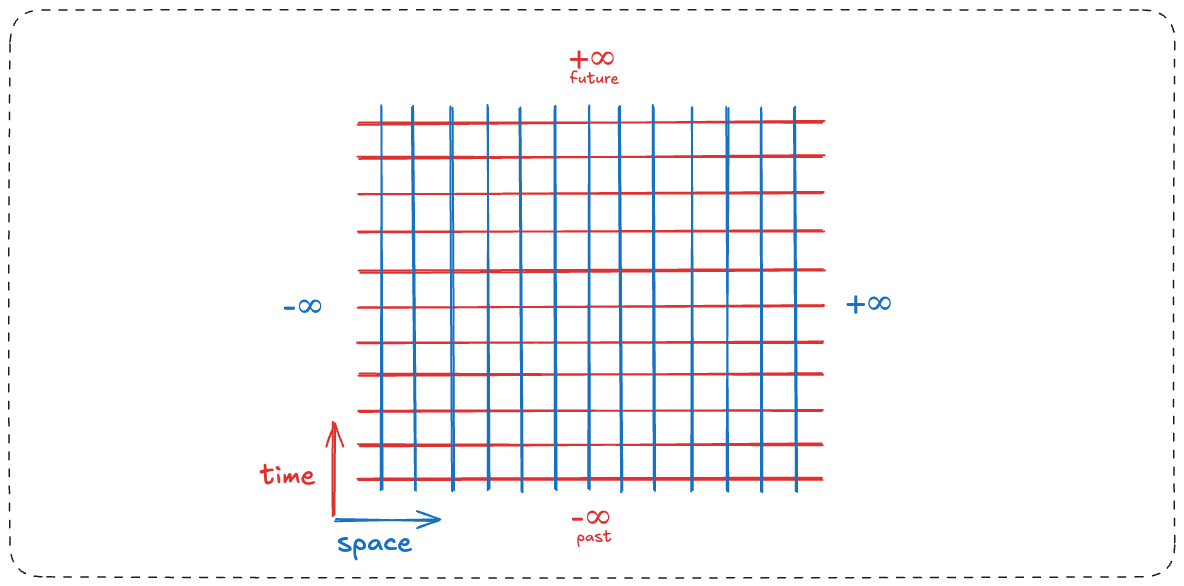
Once again we are removing dimensions of space to make this drawable. There is one dimension of space (blue) and one dimension of time (red).
Each red tick represents passing time, and blue is a position in space. A similar grid is used for drawing Light Cones.
We can do a mathematical transformation and compactify the grid, by converging the distant infinities to a point.
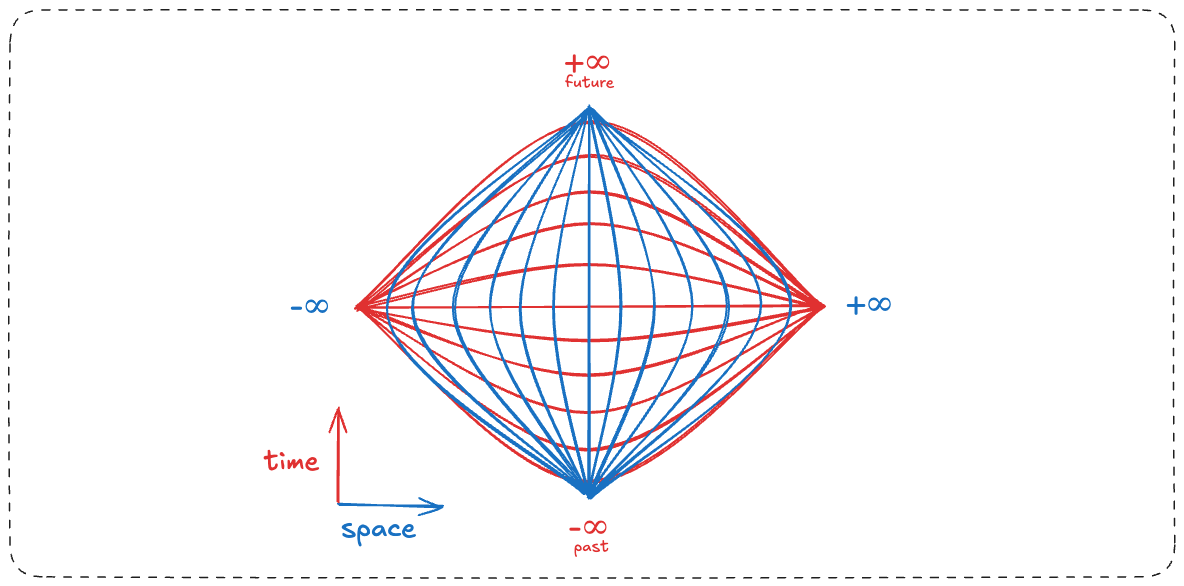
It is possible to converge because of infinite scale. Think about endlessly zooming into a fractal. Because numbers are infinitely divisible - just as they can infinitely grow - you can zoom in forever on the convergent points and never reach a point where the gaps disappear.
But something strange has occurred - there now appears to be a boundary on the infinite grid.
An infinite universe now has an edge.
Let’s look at a more detailed diagram to see what this represents.
Penrose Diagram
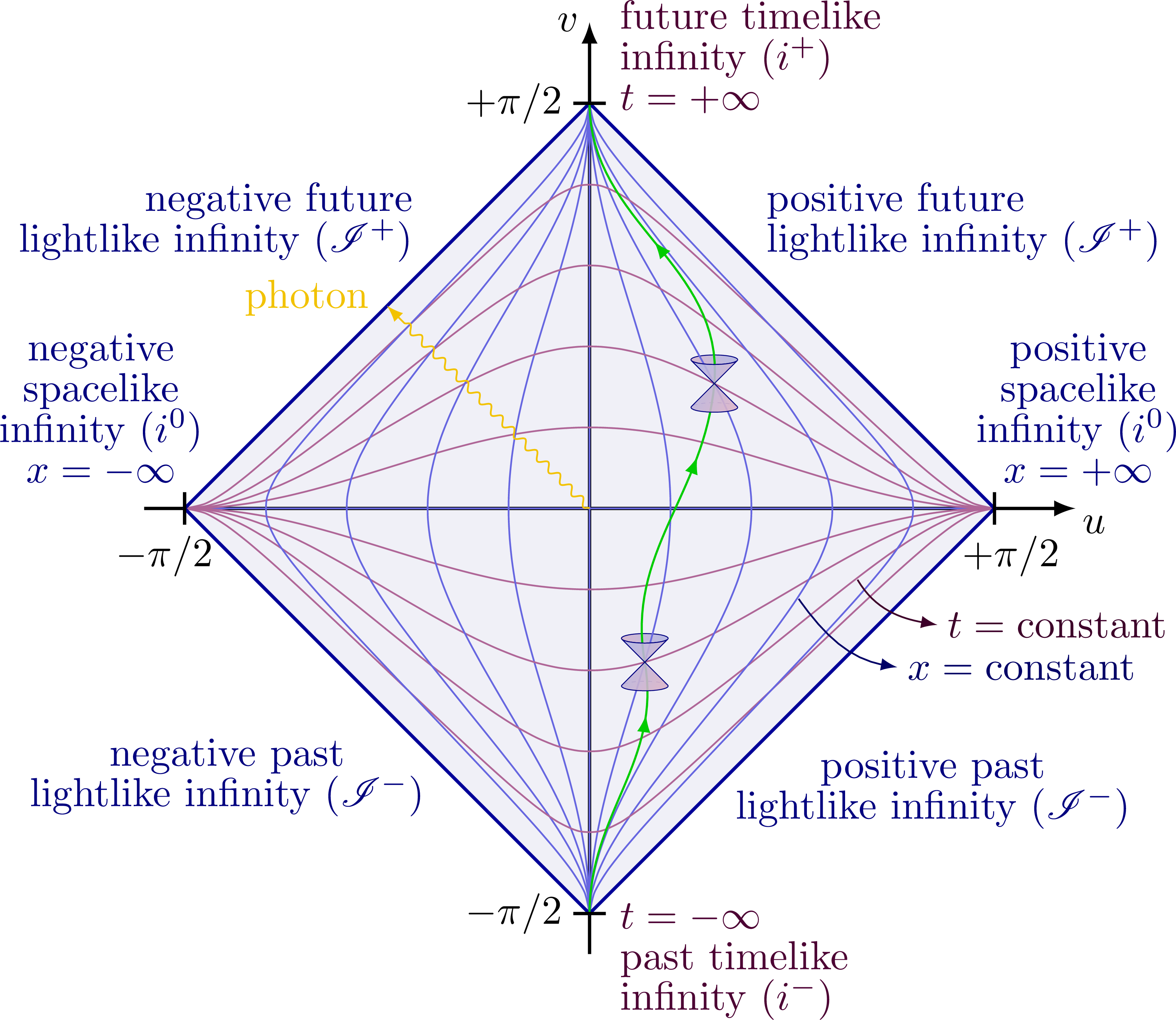
This is a Penrose Diagram - thought of by Roger Penrose in order to do calculations on black holes - they provide enhanced ways to represent concepts like the event horizon and singularity. The Penrose Diagram is made in Minkowski Space, a “flat” universe.
An important property is that it is conformal - the transformation preserves all internal angles, and angles between intersecting lines stay the same. Each “square” in the diagram represents the same “area” of spacetime.
Light will always travel at a 45 degree angle in this diagram - same as a Light Cone. You can draw light cones to determine Causality within the diagram.
The green path in the diagram above represents any object’s (sub-lightspeed) trajectory in the universe. They always emerge from the past convergence - and no matter how curved the path - will end up at the future one. All sub-lightspeed objects remain in space due to having mass. Only light and other massless entities (like quantum fields) can reach the boundaries.
Convergence Points
The convergence points represent infinities. In the time dimension - the bottom point represents all of space in the infinite past. The top is all of space in the infinite future.
Lightlike infinity
So how can light travel 45 degrees to the boundary - and what does this boundary represent?
These boundaries are also call null infinities.
To understand what this means, think about each dimension independently. You can move an infinite amount of distance on one, and an infinite amount of time on the other. Moving to the boundary represents doing both.
At it’s limit - it’s describing where all light rays “start from” and “end up” - somewhere an infinite distance away, an infinite amount of time in the past or future.
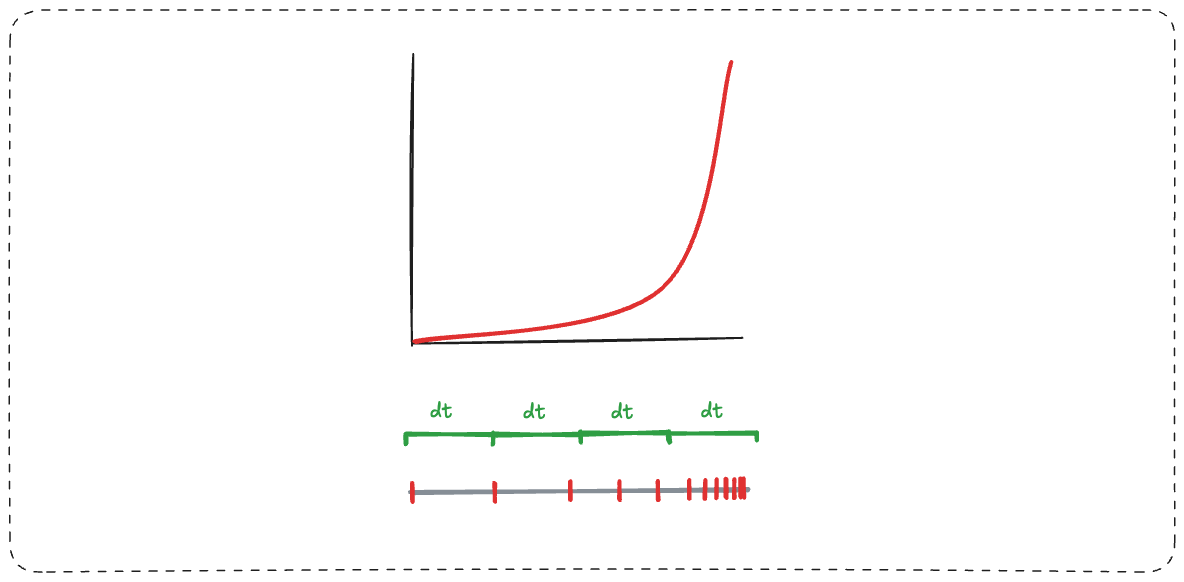
Zeno's Universe
A similar trick is going on when we draw Zenos Paradox on a piece of paper.
You draw a line from 0 to 1, and then a series of ticks that get closer and closer together.
The Penrose diagram is performing this trick at the boundaries. You can’t actually draw infinite ticks, but you can represent them in a non infinite space. This is because 0 to 1 is the inverse of 1 to ∞.
The conformal grid is essential to understanding the Falling into a Black Hole. In Minkowski Space it is useful for calculations - performing this transformation in curved AdS Space has much deeper consequences.