Three possible curvatures.
Types of Geometry
When analyzing the shape of our universe, theres really only three geometries.
To simplify, lets start by just thinking about a lens.
We understand that a lens can only come in three varieties: convex, flat, and concave.
Let’s also look on the effect they have on light that passes through them.
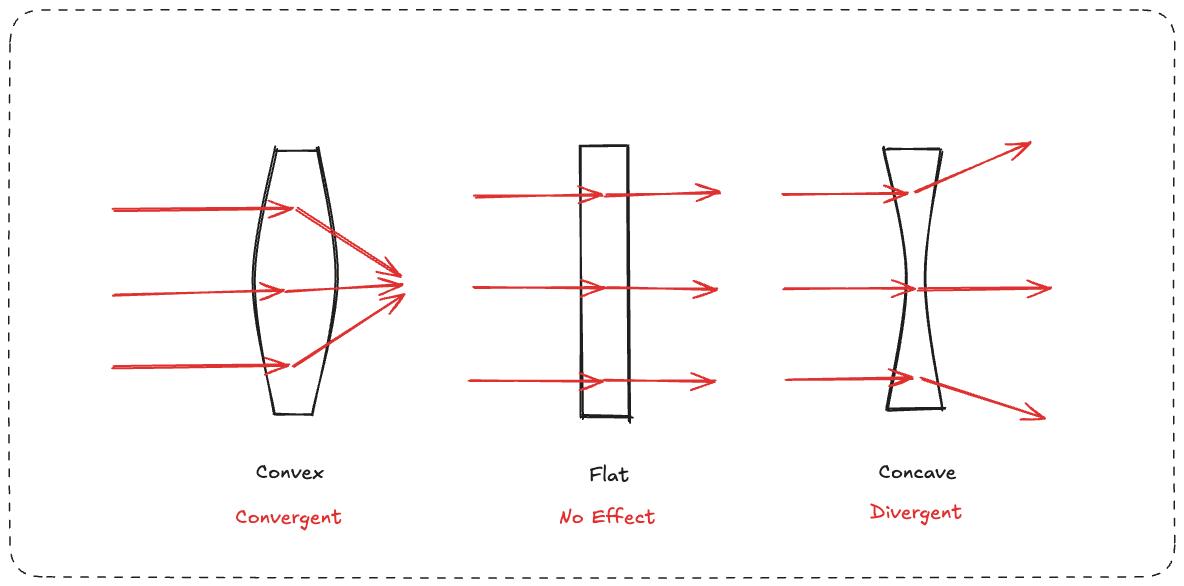
This is to point out that in terms of geometry, you can only have these three: Divergent, Convergent, and No change.
Let’s expand on this idea.
Types of Universe
In order to visualize the higher dimensions of our universe - we will use 2D surface analogs.
Closed Universe
The only type of non-infinite universe is one that has a “positive curvature”, meaning it curves back on itself. It’s like the 3D analog of the 2D surface of a sphere. Travel far enough and you’ll eventually end up back where you started.

Geometry is a bit broken because of geodesics - straight lines on a curved surface. Parallel lines will curve towards each other before crossing and looping back around. Geodesics are better explained in General Relativity.
This is a convergent shape - like the convex lens above.
A universe with this geometry is called deSitter Space.
Flat Universe
This universe is flat - meaning parallel lines stay parallel - and they go on forever. This universe is infinite.

This is a flat shape, like the flat lens above. This is called Minkowski Space.
Hyperbolic Universe
This universe has “negative curvature”. The 2D analog of this is the hyperbolic surface - like an infinite horse saddle - or pringle. Remember, a hyperbola is the inverse of a circle.

In this geometry, parallel lines with diverge from each other - like the concave lens.
Because it is the opposite of the convergent shape this is known as Anti-deSitter Space - or AdS Space.